

The sign of the trigonometric ratios change based on the value of θ.So there are 2 important things to remember.
TRIGONOMETRIC IDENTITIES FORMULAS SHEET FULL
For 180 o ± θ and for 360 o ± θ, the signs will remain the same.įor 3600+θ, the angle will complete one full rotation and then lie in quadrant 1 where all trigonometric ratios are positive. 2700-θ will fall in the quadrant 3 and in this quadrant trigonometric ratios of tan and cot are positive, so it will again be negative. This is because any angle that is 2700+θ will fall in quadrant 4 and in this quadrant only trigonometric ratios of cosĪnd sec are positive. We need to understand that trigonometric ratios would change for angles- 90 o ± θ and 270 o ± θ and they will remain same for 180 o ± θ and 360 o ± θ. Let’s see what happens when we add or subtract θ from 90 o ± θ and 270 o ± θ We know that in quadrant 4, only cosθ and secθ will be positive, the others will be negative, therefore. If we move in the clockwise direction, the angle will be taken as – θ. Θ is the angle made between the x-axis and the line, in the anti-clockwise direction.
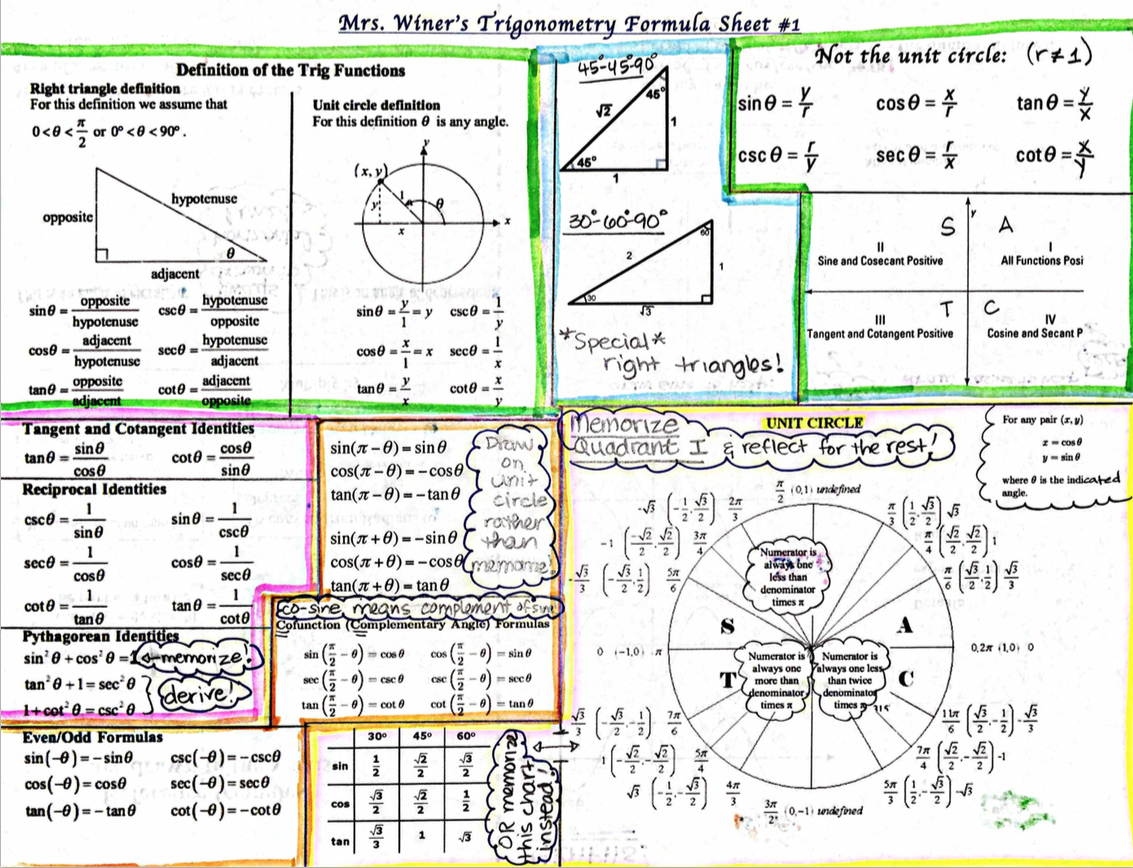
In Q4 all trigonometric ratios of tanθ and cotθ are positive.In Q3 all trigonometric ratios of cosθ and secθ are positive.In Q2 all trigonometric ratios of sinθ and cosecθ are positive.In Q1 all Trigonometric Ratios are positive.So let us see how signs change with respect to the quadrant they lie in. Let us assume an angle of θ1 lying in the 1st quadrant and an angle θ in quadrant one and two combined. The sign is based on the quadrant in which the angle lies. Therefore it becomes extremely essential for us to understand how trigonometric ratios get the positive or negative If you know one acute angle and one of the three sides, you can find the other acute angle and the other two sides.Ī lot of trigonometry formulas are based on the signs of trigonometric ratios, based on the quadrants they lie in.If you know two of the three sides, you can find the third side and both acute angles.
TRIGONOMETRIC IDENTITIES FORMULAS SHEET PDF
Trigonometric Formulas PDF Square Law FormulasĪlong with the knowledge that the two acute angles are complementary, that is to say, they add to 90°, you can solve any right triangle: Magical Hexagon for Trigonometry Identities The trigonometric properties are given below (Perpendicular) 2 + (Base) 2 = (Hypotenuse) 2 Pythagorean theorem, the well-known geometric theorem that the sum of the squares on the legs of a right triangle is equal to the square on the hypotenuse (the side opposite the right angle)-or, in familiar algebraic notation, (P) 2 + (B) 2 = (H) 2Īpplying Pythagoras theorem for the given right-angled theorem, we have: If θ is one of the acute angles in a triangle, then the sine of theta is the ratio of the opposite side to the hypotenuse, the cosine is the ratio of the adjacent side to the hypotenuse, and the tangent is the ratio of the opposite side to the adjacent side

The most important formulas for trigonometry are those for a right triangle. To convert from degrees to radians, multiply the number of degrees by π/180. The length of the arc is just the radius r times the angle θ where the angle is measured in radians. You can easily find both the length of an arc and the area of a sector for an angle θ in a circle of radius r. The identities don’t refer to particular geometric figures but hold for all angles. These formulas relate lengths and areas of particular circles or triangles. Trigonometric Ratiorelationship between the measurement of the angles and the length of the side of the right triangle. Geometrically, these are identities involving certain functions of one or more angles.

Trigonometric Identities are equalities that involve trigonometric functions and are true for every value of the occurring variables where both sides of the equality are defined. Trigonometry formulas are essential for solving questions in Trigonometry Ratios and Identities in Competitive Exams. Maths Formulas – Trigonometric Ratios and identities are very useful and learning the below formulae help in solving the problems better. Trigonometry is a branch of mathematics that deal with angles, lengths and heights of triangles and relations between different parts of circles and other geometrical figures.


 0 kommentar(er)
0 kommentar(er)
